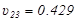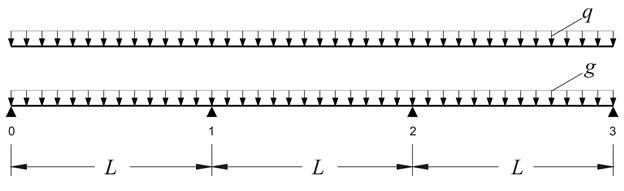
Η συνεχής πλάκα του σχήματος έχει σε κάθε άνοιγμα μήκος L=5.00 m και πάχος h=160 mm, ενώ καταπονείται από φορτίο επικάλυψης ge=1.0 kN/m2 και ωφέλιμο q=5.0 kN/m2. Σκυρόδεμα C50/60. Ζητείται η περιβάλλουσα των ροπών και των τεμνουσών, σε οριακή κατάσταση αστοχίας, των τριών πλακών.
Επίλυση:
Ίδιο βάρος: go=0.16m×25.0kN/m3= 4.00 kN/m2
Επικάλυψη: ge= 1.00 kN/m2
Σύνολο μόνιμων φορτίων: g= 5.00 kN/m2
Σύνολο ωφέλιμων φορτίων: q= 5.00 kN/m2
Το μόνιμο φορτίο σχεδιασμού κάθε πλάκας ισούται με gd=1.00×5.0=5.0 kN/m και το συνολικό φορτίο σχεδιασμού με pd=γg×g+γq×q=1.35×5.0+1.50×5.0=14.25 kN/m.
Επίλυση με το χέρι:
I=(b×h3)/12=(1.0×0.163)/12=341×10-6 m4
Το μέτρο ελαστικότητας για σκυρόδεμα C50/60 ισούται με E=37.3 GPa.
E×I=37.3×109N/m2×341×10-6m4=12.719×106 N×m2
Επειδή I10=I12=I23=Ic, οι συντελεστές δυσκαμψίας k και οι δείκτες κατανομής υ ισούνται με:

Λόγω συμμετρίας φορέα: 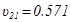 ;και
;και