|
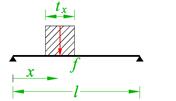
Αμφιαρθρωτή πλάκα
|
|
bm,f = ty + 2.5×x×(1-x/l)
tx,max = l, ty,max = 0.8l
|
bm,vL = ty + 0.5×x
tx,max = l, ty,max = 0.8l
bm,vR = ty + 0.5×(l-x)
tx,max = l, ty,max = 0.8l
|
|
Παράδειγμα 1
|
bm,f=0.37+2.5×1.5×(1-0.375)=2.71 m
|
bm,vL=0.37+0.5×1.5=1.12 m
bm,vR=0.37+0.5×2.5=1.62 m
|
|
Παράδειγμα 2
|
bm,f=0.37+2.5×2.0×(1-0.5)=2.87 m
|
bm,vL=0.37+0.5×2.0=1.37 m
bm,vR=0.37+0.5×2.0=1.37 m
|
|
Μονόπακτη πλάκα
|
|
bm,f = ty + 1.5×x×(1-x/l)
tx,max = l, ty,max = 0.8l
bm,s = ty + 0.5×x×(2-x/l)
tx,max = l, ty,max = 0.8l
|
Left: για 0.2<x/l<1
bm,vL = ty + 0.3×x
tx,max = 0.2l, ty,max = 0.4l
Right: για 0<x/l<0.8
bm,vR = ty + 0.4×(l-x)
tx,max = 0.2l, ty,max = 0.4l
|
|
Παράδειγμα 1
|
bm,f=0.37+1.5×1.5×(1-0.375)=1.78 m
bm,s=0.37+0.5×1.5×(2-0.375)=1.59 m
|
bm,vL=0.37+0.3×1.5=0.82 m
bm,vR=0.37+0.4×2.5=1.37 m
|
|
Παράδειγμα 2
|
bm,f=0.37+1.5×2.0×(1-0.5)=1.87 m
bm,s=0.37+0.5×2.0×(2-0.5)=1.87 m
|
bm,vL=0.37+0.3×2.0=0.97 m
bm,vR=0.37+0.4×2.0=1.17 m
|
|
Αμφίπακτη πλάκα
|
|
bm,f = ty + x×(1-x/l)
tx,max = l, ty,max = 0.4l
bm,sL = ty + 0.5×x×(2-x/l)
bm,sR = ty + 0.5×(l-x)×(1+x/l)
tx,max = l, ty,max = 0.4l
|
bm,vL = ty + 0.3×x
tx,max = 0.2l, ty,max = 0.4l
bm,vR = ty + 0.3×(l-x)
tx,max = 0.2l, ty,max = 0.4l
|
|
Παράδειγμα 1
|
bm,f=0.37+1.5×(1-0.375)=1.31 m
bm,sL=0.37+0.5×1.5×(2-0.375)=1.59 m
bm,sR=0.37+0.5×2.5×(1+0.375)=2.09 m
|
bm,vL=0.37+0.3×1.5=0.82 m
bm,vR=0.37+0.3×(4.0-1.5)=1.12 m
|
|
Παράδειγμα 2
|
bm,f=0.37+2.0×(1-0.5)=1.37 m
bm,s=0.37+0.5×2.0×(2-0.5)=1.87 m
bm,sR=0.37+0.5×2.0×(1+0.5)=1.87 m
|
bm,vL=0.37+0.3×2.0=0.97 m
bm,vR=0.37+0.3×(4.0-2.0)=0.97 m
|
|
Πρόβολος πλάκα
|
|
bm,s = ty + 1.5×x
tx,max = l, ty,max = 0.8l
|
για 0.2<x/l<1
bm,v = ty + 0.3×x
tx,max = 0.2l, ty,max = 0.4l
|
|
Παράδειγμα 1
|
bm,s=0.37+1.5×1.5=2.62 m
|
bm,v=0.37+0.3×1.5=0.82 m
|
|
Παράδειγμα 2
|
bm,s=0.37+1.5×2.0=3.37 m
|
bm,v=0.37+0.3×2.0=0.97 m
|
|