Τετραέρειστες-Τριέρειστες-Διέρειστες

Όταν μία πλάκα στηρίζεται και στις τέσσερις παρυφές και ο λόγος του μεγαλύτερου προς το μικρότερο θεωρητικό άνοιγμα είναι ≤2.00, θεωρείται τετραέρειστη.
Οι τετραέρειστες πλάκες υπό ομοιόμορφο φορτίο επιλύονται στατικά με πίνακες, από τους οποίους προκύπτουν οι θεμελιώδεις ροπές στηρίξεων, οι ροπές ανοιγμάτων και οι τέμνουσες δυνάμεις.
Στους πίνακες αυτούς, ανάλογα με τον τρόπο στήριξης, κάθε πλάκα χαρακτηρίζεται από έναν αριθμό από 1 έως 6, όπως απεικονίζεται στο σχήμα.
Το διάφραγμα ενός ορόφου περιλαμβάνει κατά κανόνα πολλές πλάκες σε επαφή μεταξύ τους και η κάθε πλάκα επηρεάζει τις υπόλοιπες. Ο ακριβής υπολογισμός των επιρροών αυτών πραγματοποιείται μόνο με τη χρησιμοποίηση επιφανειακών πεπερασμένων στοιχείων. Στις συνήθεις περιπτώσεις, οι γειτονικές πλάκες δεν επηρεάζουν σημαντικά τις τέμνουσες δυνάμεις και τις αντιδράσεις μίας τετραέρειστης πλάκας. Για το λόγο αυτό, και για να είναι εφικτός ο υπολογισμός με απλά υπολογιστικά μέσα, εξετάζουμε κάθε πλάκα χωριστά.

Η κατανομή του φορτίου είναι τριγωνική ή τραπεζοειδής. Τα ύψη των τριγώνων/τραπεζίων ορίζουν τις μέγιστες τιμές του φορτίου που μεταβιβάζεται στα αντίστοιχα σημεία της περιμετρι-κής στήριξης. Τα μέγιστα αυτά φορτία είναι οι μέγιστες τέμνουσες δυνάμεις Vi,j της πλάκας, ενώ τα ισοδύναμα φορτία pi,j είναι οι ισοδύναμες ομοιομορφισμένες αντιδράσεις.

Οι τιμές των συντελεστών των τεμνουσών δυνάμεων V_i,j και των ισοδύναμων ομοιόμορφων αντιδράσεων p_i,j δίνονται στους έξι πίνακες b5.1 έως b5.6 που παρατίθενται στο τέλος του βι-βλίου. Σε καθεμία από τις έξι περιπτώσεις στηρίξεων σχηματίζονται δύο τρίγωνα και δύο τραπέζια κατά τις διευθύνσεις x, y ή αντίστροφα (ανάλογα με το λόγο των πλευρών).

Shear force diagram by Czerny for side ratio 1.50

According to the theory of elasticity, the distribution of shear forces along the length of the four edges of a slab, results from the shear forces along its perimeter as described by equations. The most unfavourable shear forces along the sides of a slab (as well as the most unfavourable bending moments) are tabulated in the tables of the book entitled “Applications of Reinforced Concrete” (p46-51 for two-way slabs, p52-59 three- or two-side-supported slabs) of series of books by Apostolos Konstantinidis published in1994.

In this method, the slab is replaced by two intersecting strips along directions x and y respectively, which meet in its middle point m.

Depending on the support conditions, the strips are classified as simply supported, fixed at one end or fixed at both ends.

The coefficients used for the determination of spans and supports bending moments result from the tables depending on the aspect ratio (where in lx is the shortest dimension) and the type of support. 

Thus:

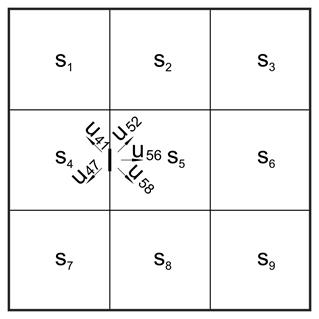
Stiffness coefficients and transfer indices of each slab depend on its type of support and its aspect ratio. These data are provided by tables in several books, e.g. by Hahn.

All supports are considered fixed when principal moments are calculated.

One support is freed, e.g. 45 of the figure, and distribution takes place on all directions (i.e. CROSS method on plane).

This procedure is repeated until moments balance.

Such a solution is, certainly, complex and laborious, but it is applicable in case of large spans with significant differences in dimensions and thicknesses.

In usual cases of slabs with almost the same thickness (even for large or uneven spans), support moments are calculated with reasonable accuracy according to the expression:

, where  and  are the principal moments at support 1.

Support moments affect at minimum level span moments, resulting the latter to be calculated considering rigid supports.

This particular method is applied in the majority of practical problems, as it combines adequate accuracy (much more accurate than the strip method) with high speed application.

The general case of unfavourable loadings is described in §4.2.3 for every type of slab. This paragraph focuses on imposing and determining unfavourable loadings in the special case of a symmetric group of two-way slabs.

Unfavourable loadings are always considered as of zatrikion (chess) form. This property leads to the consideration of two equivalent loading cases, one with uniform positive loads of equal magnitude and another of zatrikion form with uniform loads of equal magnitude but alternating sign.

This technique is applied in the next example. It is worth noting that the paragraph containing the exercises of this chapter deals with the analysis of a large symmetric group of two-way slabs.

A three-edge-supported slab is the one supported along three edges.

Static analysis is performed similar to two-way slabs (i.e. considering each individual slab), by means of tables e.g. by Hahn.

Moments are practically distributed according the approximate method of § 4.6.3.3.

The tables support global uniform loads, continuous linear uniform loads on free edges and continuous linear moments on free edges.

A slab of shape Γ

is analyzed considering one three-edge-supported slab and one two-way slab, as shown in figure below. This method is proposed by Hahn and it requires particular attention reinforcing the slab. Indicatively, it is emphasized that continuous reinforcement should be placed along the lower fibers at the theoretical boundary of the two-way slab and the three-edge-supported slab.

A two-edge-supported slab is the one supported on two adjacent edges.

Static analysis is performed similar to two-way slabs, by means of tables e.g. by Stiglat.

Special attention should be paid to the reinforcement distribution, which has to be compatible with that of the corresponding moment distribution.

Near edges, these slabs behave practically as cantilevers (of course depending on the aspect ratio l_y/l_x), such as the slab section with length l_x-l_y illustrated in the figure.