Gravity Loads

In every building like the one shown in the above figure, permanent (dead) and imposed (live) loads are applied. The latter are much lower than the former, for example 3 persons and the living-room furniture weight as much as a single m2 of slab surface while a car weights as much as a sole beam. Structure loads can be classified into three categories gravity loads, seismic loads and wind loads.

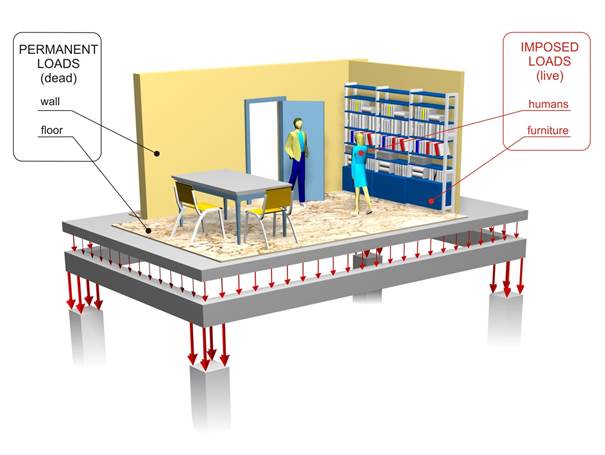
The structural frame is designed to continuously withstand the vertical gravitational loads (self-weight, masonry walls, floor coverings, cars, furniture, people etc) and, not in a continuous but in a periodical basis, the wind and snow actions. Moreover it must always bear the “self-induced” loadings caused by temperature changes etc.

Apart from the usual loads, in earthquake prone regions, the structural frame must have enough strength surplus distributed in such a way so that in the critical moment of an earthquake, to be able to respond successfully, retaining the building intact.

The density and the related unit weight of the materials used in construction are:
Reinforced concrete ρ=2.50 t/m3 (ε=25.0 kN/m3)
Light- weight concrete for ground leveling ρ=0.80 t/m3 (ε=8.0 kN/m3)
Sand mortar ρ=2.00 t/m3 (ε=20.0 kN/m3)
Marble ρ=2.70 t/m3 (ε=27.0 kN/m3)
The dead mass of one m2 of the above slab is,
g = 0.15*2.50 + 0.04*0.8 + 0.02*2.0 + 0.02*2.7 = 0.5 t,
i.e. the self mass of one square meter of a usual slab is 0.5 t (weight 5.0 kN)

ρ = 1.00 t/ m3 (ε = 10.0 kN/m3)
The dead mass of one m2 of a pool slab, when the pool is filled with just 1.0 m of water is,
1.4 t (weight 14.0 kN)

ρ = 2.50 t/m3 (ε = 25.0 kN/m3)
The dead mass of one m2 of a slab, with 1.0 m of soil on top is 2.5 t (weight 25.0 kN)

Masonry stretcher bond ρ = 0.21 t/m² (ε = 2.1 kN/m²)
Masonry Flemish bond ρ = 0.36 t/m² (ε = 3.6 kN/m²)

A wall of 1.00 m length, 2.85 m height and 100 mm thickness has a mass equal to 0.6 t. (weight 6.0 kN).

ρ = 0.20 t/m² (ε = 2.0 kN/m²)
The live mass of one m2 residential building is 0.2 t (weight 2.0 kN)

ρ = 0.50 t/m² (ε = 5.0 kN/m²)
The live mass of one m² commercial area is 0.5 t (weight 5.0 kN)

As a rule, snow loading is lower than the live load generated by the use of people and its value ranges between 0.60 and 1.50 kN/m².

ρ = 0.25 t/m² (ε = 2.5 kN/m²)
The live distributed load of 1 m² of a parking space is 0.25 t (weight 2.5 kN)

In a residential building, the maximum live loads are about 20% of the dead loads

In random cases like earthquakes, the extensive live loads may reach 6% of the dead loads