Structural model

l_eff=l_n+α_left+α_right  where α=min(t/2,h/2)

·         At the end support of the first slab, the width is considered to be a=t₁/2=125 mm which is acceptable as in favor of the safety.

·         The width of beam-column supports, is taken into account more efficiently, when the analysis uses rigid bodies (see next paragraph).

Continuous beam: l_o distance between consecutive points of zero moments 

Continuous frame beam: l_o distance between consecutive points of zero moments

Earthquake resistant structures require strong columns and fixed column-beam connections. This requirement demands the creation of a frame set of beams, forming a continuous structure with respect to geometry, but autonomous with respect to the adjacent beams. This fact leads to the conclusion that, in general, the supports of a beam are rarely pinned. Therefore, l_o=0.70×l can be chosen for all the earthquake resistant beams.

b_eff=b_w+b_eff,1+b_eff,2≤b_lim where b_eff,1=0.20×b₁+0.10×l_o≤0.20×l_o and b_eff,2=0.20×b₂+0.10×l_o≤0.20×l_o.

·         Τhe effective widths at supports have practical meaning mainly for the dimensioning of  inverted concrete beams under bending.

·         When an adjacent slab is cantilever, of a span l_n, the corresponding b₁ or b₂ is equal to l_n.

The actual structure and the space model (screen shot captured by HoloBIM)

The space frame model comprises nodes (e.g. node 1, 5, 9 etc.) and members (e.g. member 1, 2, 5 etc.). Nodes are symbolic geometric points where members end. 

In general, each node has 6 displacements (6 degrees of freedom), three translations δx, δy, δz and three rotations φx, φy, φz. The objective of the analysis is the calculation of the 6 displacements for all nodes.

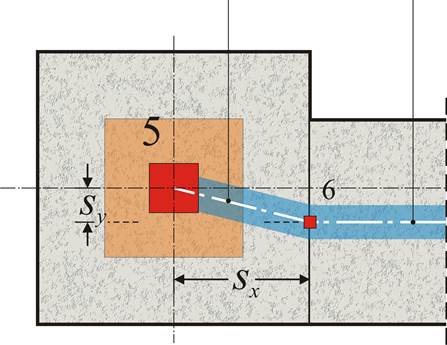
Plan and 3D of column-beam nodes: Master node (5) and slave node (6)

Provided the 6 displacements of the master node are δx, δy, δz, φx, φy, φz, the corresponding δx,s, δy,s, δz,s, φx,s, φy,s, φz,s of the slave node are:

φ x,s = φ x , φ y,s = φ y , φ z,s = φ z , δ x,s = δ x -sy × φ z (given sz=0), δ y,s = δ y +sx × φ z (given sz=0),

δ z,s = δ z -sx × φ y +sy × φ x

Diaphragmatic behaviour of floor and the displacements of a random point i of the diaphragm due to φz

The 3 displacements δz, φx, φy of each node belonging to the diaphragm are independent of each other, while the rest δx, δy, φz are depended on the 3 displacements of point CT called Center of Elastic Torsion of the diaphragm. Displacements δxi, δyi, φzi at the point i of the horizontal diaphragm are expressed as: