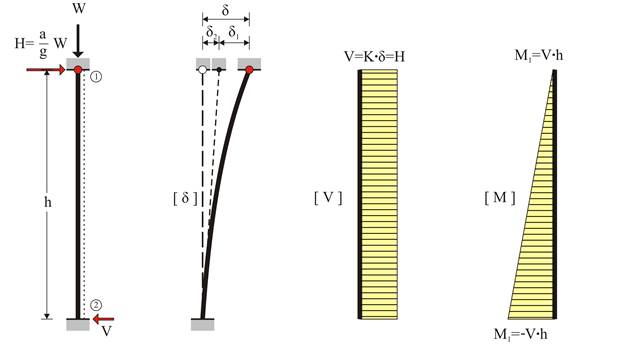
One-end-fixed column: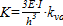
The fixity degree of a column end, in a specific direction, depends on the relative stiffness between the column and its framing beams.
The fixity degree varies from fixed to pinned. When a weak column (e.g. cross-section 300/300) is connected to strong beams (e.g. concrete beams with height 800mm) the connection could be considered as fixed. On the contrary, when the column top is connected to a plain slab and the column base is connected to weak footing in soft soil without foundation beams, the connections could be idealised as pinned.