Space frames

Simple one-storey structure comprising four columns whose tops are connected by rigid slab-diaphragm

Floor slabs act in storey frames as strong horizontal elements, called diaphragms. Diaphragms are practically rigid and non-deformable and thus impose specific movements to the beams and the column tops.

In case of an earthquake event, during which the main stresses are induced by the horizontal seismic actions, diaphragm action affects directly the behaviour of the whole structure.
The diaphragmatic behaviour of structures of any type and size is presented in the following par-agraphs. The simple four-column structure of the previous page is used as an example.

The centre of mass C_M and the equivalent mass inertial ring with radius of gyration l_s

The inertial behaviour of a diaphragm having a mass Σ(m_i) is  idealised by a ring of equivalent inertial mass distribution. The ring has a total mass Σ(m_i), its centre is the Centre of Mass C_M and its radius the Radius of Gyration l_s.

The coordinates of the centre of mass C_M of a diaphragm consisting of many mass points, linearly distributed, and surface masses linearly distributed derive from the expressions:

,                                                                                  (1)

The radius of gyration l_s of the diaphragm with respect to the centre of mass C_M derives from the expression:

                                                                                                                        (2)

where Χ_i and Υ_i are the coordinates of each mass point m_i of the diaphragm, whereas I_pi is the polar moment of inertia of each mass m_i  with respect to the centre of mass C_M.

Centre of mass:

Due to symmetrical mass distribution, X_CM=3.0 m and Y_CM=2.5 m.

Radius of gyration: [g=10 m/sec², therefore force F=1 kN corresponds to mass m=0.1 t.]

Slab: m₁=6.0m·5.0m·0.71t/m²=21.3 t

b₁=6.0 m, l₁=5.0 m, L₁=0.0 m → I_p1=21.3t·(6.0²+5.0²)m²/12=108.3 t·m²

Beam connecting C₁-C₂: m₂=6m·1.0t/m=6.0 t, l₂=6.0 m, L₂=2.5 m → I_p2=6.0·(6²/12+2.5²)=55.5 t·m²

Beam connecting C₃-C₄: likewise m₃=6.0 t, I_p2=55.5 t·m²

Beam connecting C₁-C₃: m₄=5.0m·1.0t/m=5.0 t, l₄=5.0 m, L₄=3.0 m → I_p4=5.0·(5.0²/12+3.0²)=55.4 t·m²

Beam connecting C2-C4: likewise m₅=5.0 t, I_p5=55.4 t·m²

Columns: m₆=0.1·(4.00+4.00+6.0+4.5)=1.85 t, L₆=√ (3.0²+2.5²)=3.905 m →  I_p6=1.85·3.905²=28.2 t·m².

Simple one-storey structure comprising four columns, whose tops are connected by a rigid slab-diaphragm

The current paragraph examines the special case of orthogonal columns in parallel arrangement. The general case is examined in Appendix C.

Χ0Υ initial coordinate system, xC_Ty main coordinate system

When a horizontal force H acts on a storey level, all the points of the slab including the column tops move in accordance with the same rules due to the in-plane rigidity of the slab.

These rules induce the diaphragm to develop a parallel (translational) displacement by δ_xo, δ_yo and a rotation θ_z about the centre of stiffness C_T(x_CT, y_CT) in xC_Ty coordinate system, which is parallel to the initial coordinate system X0Y and has as origin the point C_T.

The diaphragmatic behaviour may be considered as a superposition of three cases:

(a) parallel translation of the diaphragm  along the X direction due to horizontal force component H_X,

(b) parallel translation of the diaphragm  along the Y direction due to horizontal force component H_Y,

(c) rotation of the diaphragm due to moment M_CT applied at the centre of stiffness C_T.

In case a horizontal force H_x is applied at C_T in x direction, the following 2 equilibrium equations apply:

·         The sum of forces in x direction is equal to H_x, i.e. H_x=Σ(V_xoi) (i).

·         The sum of moments V_xoi about the point C_T is equal to zero, i.e. Σ(V_xoi·y_i)=0 (ii).

Each column i carries a shear force V_xoi=δ_xo·K_xi.

Σ(V_xoi)=Σ(δ_xo·K_xi)=δ_xo·Σ(K_xi),  expression (i) gives H_x=δ_xo·Σ(K_xi) →

H_x=K_x·δ_xo where K_x=Σ(K_xi).

Expression (ii) gives Σ(V_xoi·[Y_i-Y_CT])=0 → Σ(V_xoi·Y_i )-Σ(V_xoi·Y_CT)=0 → Y_CT·Σ(V_xoi)= Σ(V_xoi·Y_CT) →

Y_CT=Σ(δ_xo·K_xi·Y_i)/Σ(δ_xo·K_xi) → Y_CT=Σ(K_xi·Y_i)/Σ(K_xi)

Accordingly, the corresponding expressions are derived for direction y.

H_y=K_y·δ_yo where K_y=Σ(K_yi) and X_CT=Σ(K_yi·X_i)/Σ(K_yi)

Summarising, the centre of stiffness and the lateral stiffnesses are defined by the following expressions:

Centre of stiffness and lateral stiffnesses:

, where    

(4’)
, where      

(5’)

To determine the deformation developed by external moment M, applied at the centre of stiffness C_T, the initial system X0Y is transferred (by parallel translation) to the principal system xC_Ty. The centre of mass is transferred to the principal system along the structural eccentricities e_ox, e_oy in accordance with the following expressions:

Principal coordinate system

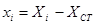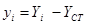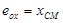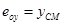,  ,   ,                                                              (6’)

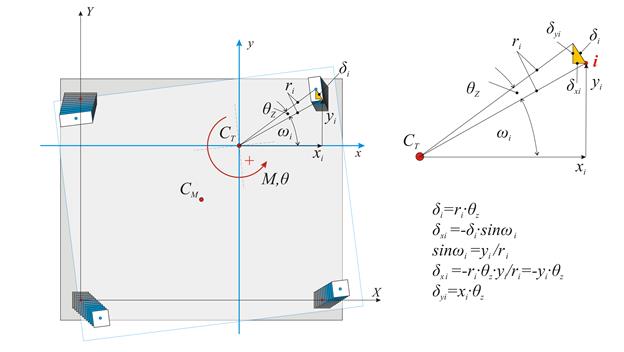
The displacement of the diaphragm consists essentially of a rotation θ_z about the C_T, inducing a displacement δ_i at each column top i with coordinates x_i,y_i in respect to the coordinate system with origin the C_T. If the distance between the point i and the C_T is r_i, the two components of the (infinitesimal) deformation δ_i are equal to δ_xi=-θ_z·y_i and δ_yi=θ_z·x_i.

The shear forces V_xi and V_yi in each column developed from the displacements δ_xi, δ_yi are:

V_xi=K_xi·δ_xi=K_xi·(-θ_z·y_i) → V_xi=-θ_z·K_xi·y_i and V_yi=K_yi·δ_yi=K_yi·(θ_z·x_i) → V_yi=θ_z·k_yi·x_i

The resultant moment of all shear forces V_xi, V_yi about the centre of stiffness is equal to the external moment M_CT, i.e.

M_CT=Σ(-V_xi·y_i+V_yi·x_i+K_zi) → M_CT= θ_z·Σ(K_xi·y_i²+K_yi·x_i²+K_zi)

Torsional stiffness K_zi of column i

Columns resist the rotation of the diaphragm by their flexural stiffness expressed in terms K_xi·y_i² , K_yi·x_i² (in N·m), and their torsional stiffness K_zi, which is measured in units of moment e.g. N·m.

The  torsional stiffness of a column is given by the expression  K_z=0.5E·I_d/h, where 0.5Ε is the material shear modulus G, usually taken equal to 0.5 of the elasticity modulus, h is the height of the column and I_d is the torsional moment of inertia of the column’s cross-section, taken from the following table.

Torsional stiffness of the floor diaphragm

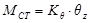, where  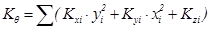                                                       (7’)

The quantity Κ_θ is the torsional stiffness of the diaphragm and is measured in N·m. The quantities K_x=Σ(K_xi), K_y=Σ(K_yi), measured in N/m, imply the lateral stiffnesses of the diaphragm in x and y direction respectively.

Definitions:

Lateral stiffness Κ_j of diaphragm denotes the force in direction j required to cause a relative parallel displacement of the diaphragm by one unit in considered direction.

Torsional stiffness K_θ of diaphragm denotes the moment required to cause relative rotation of the diaphragm by one unit.

Note

The torsional stiffness of columns K_z is very small and is usually omitted.

Question: Create a simple idealised equivalent structural system with the same seismic behaviour as the actual structural system.

Solution: Four idealised columns E₁, E₂ and E₃, E₄ are placed symmetrically with respect to the centre C_T and the axes x and y, i.e. all four idealised columns have the same absolute value of coordinates x and y. Each idealised column is assumed to have stiffnesses K_x=1/4·Σ(K_xi) and K_y=1/4·Σ(K_yi).

This system satisfies the two conditions of the actual system, concerning the translations of all diaphragm columns.

Stiffness by x: 4·1/4·Σ(K_xi)=Σ(K_xi) and stiffness by y: 4·(1/4)·Σ(K_yi)=Σ(K_yi)

To satisfy the third condition, the torsional stiffness of the idealised system should be

K_θ,eq=[4·(1/4)·Σ(K_yi)·y²+4·(1/4)·Σ(K_xi)·x²]=Σ(K_xi)·y²+Σ(K_yi)·x²

equal to the torsional stiffness of the actual system

K_θ,re=Κ_θ=Σ(K_xi·y_i²+K_yi·x_i²+K_zi).

i.e. K_θ,eq=K_θ,re → Σ(K_yi)·x²+Σ(K_xi)·y²=K_θ →

Torsional radii of the diaphragm:

 where   and                                                      (8’)

The curve equation (8’) is an ellipse with centre C_T, direction that of the principal axes (in this case the direction of the initial system) and semi axes r_x, r_y, (torsional radii of the diaphragm).

Conclusion:

The torsional behaviour of a floor can be described by the torsional stiffness ellipse (C_T, r_x, r_y) which represents the equivalent distribution of the diaphragm stiffness.

The radii r_x, r_y, of the ellipse are called torsional radii.

There are infinite solutions of idealised dual system sets, whose most characteristic is the one with the four idealised columns placed in the four ellipse ends.

Generally, there are infinite solutions with n-tuple diametrically opposed systems, where each idealised column stiffness is equal to 1/n of the total system stiffness.

Equivalent mass inertial ring (C_M, l_s) and torsional stiffness ellipse (C_T, r_x, r_y)

The degree of the torsional stiffness of a diaphragmatic floor is determined by the relation between the equivalent mass inertial ring (C_M, l_s) and the torsional stiffness ellipse (C_T, r_x, r_y). The optimal location of the two curves is where the torsional stiffness ellipse encloses the mass inertial ring.

A building is classified as torsionally flexible [EC8 §5.2.2.1] if either r_x<l_s or r_y<l_s is satisfied in at least one diaphragm storey level. In this example both conditions are satisfied.

For a building to be categorized as being regular in plan, the two structural eccentricities e_ox, e_oy   at each level  shall satisfy both conditions e_ox≤0.30r_x &e_oy≤0.30r_y  [EC8 §4.2.3.2]. In this particular example the first condition is satisfiede_ox=0.94 m ≤ 0.30r_x (=0.30·3.91=1.173 m), whereas the second one is not e_ox=1.34 m ≤ 0.30r_x (=0.30·3.08=0.924 m). Therefore the building that comprises that specific floor diaphragm is not regular in plan.

The structure and the model of the one-storey space frame

The analysis of the one-storey space frame illustrated in the figure, under horizontal seismic force

H=90.6 kN

is performed by means of four methods: (i) analysis using manual calculations, assuming fixed-ended columns, (ii) analysis using the Excel file, assuming fixed-ended columns, (iii) analysis using the Excel file, assuming columns with k=6, (iv) analysis using software, assuming

actual

beam and column torsional stiffnesses.

The method using manual calculations, was described via the example presented to all previous paragraphs of this chapter.
The results are identical to those of the practical calculations.
The torsional stiffness ellipse and the equivalent columns of the structure are illustrated at the end of the spreadsheetς.

The centre of stiffness, the torsional radii and the stress resultants are exactly the same as those of the previous cases, with the exception of deformations, whose relative values, however, re-main constant 12/6=2.00.

The analysis may only be performed using the software. The relevant project is <B_545>. The theory for the analytical determination of the diaphragmatic behaviour at a storey level is described in detail in Appendix D.

The equivalent mass inertial ring is the same as in the two previous methods, since it depends only on the loadings. On the contrary all other quantities are different, as expected. The centre of stiffness C_T coordinates are (3.646, 3.314), whereas the torsional stiffness radii are equal to

r_x=3.920 m

και

r_y=3.572 m

(instead of

3.910

and

3.080

respectively, assuming fixed-ended columns). The cross-section of the equivalent columns is 415/378 (instead of 524/406).