For both frames of the above structure, the calculation of the stress resultants subjected to static loads (dead and live) and seismic loads is required.
Each frame has a span of 5.0 m and a height of 3.0 m. The moment of inertia of each column member is I=0.4×0.43/12=0.0021333 m4=21.33×10-4 m4.
Τhe effective flange width of the beams is calculated according to §3.1.2: lo=0.70×l=0.70×5.00=3.50 m, b1=ln1/2=3.70/2=1.85 m, blim=bw+b1=0.30+1.85=2.15 m,
beff=min(bw+beff,1, blim)=min(0.30+0.70, 2.15)=1.00 m, since beff,1=min(0.20×b1+0.10×lo , 0.20×lo)= =min(0.20×1.85+0.10×3.50, 0.20×3.50)=min(0.72 , 0.70)=0.70 m.
From table 2 beff=1.0 m, hf/h=0.17/0.50=0.34, bw/beff=0.30 → μ=0.0417 → I=0.0417×1.0×0.503=52.125×10-4 m4
The loads on the crossbar of each frame are:
Self-weight: go=0.30m×(0.50-0.17)m×25.00kN/m3 = 2.50 kN/m
Dead loads on slab: gs=2.00m×5.25kN/m2 =10.50 kN/m
Additional dead loads: gw =20.00 kN/m
Total dead loads: g =33.00 kN/m
Live load on slab: q=2.00m×5.00kN/m2 =10.00 kN/m
Τhe self-weight of each column is 0.40×0.40×3.00×25.00=12.00 kN. Τhe 1/3 of this load (4.00 kN) is applied on the column head and the rest 2/3 of the load (8.00 kN), are applied on the column base.
The dynamic mass of each crossbar in all seismic combinations corresponds to design load:
Pd=(g+ψ2×q)×l+2columns×4.00kN=(33.00+0.30×10.00)×5.00+8.00=188.00 kN
while the seismic force applied on each crossbar is W= (ax /g)×Pd=0.65×188.00=122.00 kN.
In the following analyses implemented manually, the function of rigid bodies will not be considered. In each frame three analyses are performed, one for dead loads G, one for live loads Q and one for seismic loads in +X direction.
The general analysis of the frame subjected to vertical uniform load w, from table 1 is:
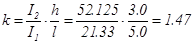
,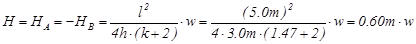
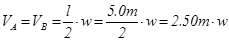
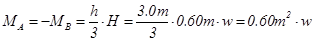
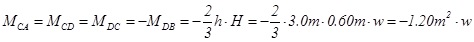
The general analysis of the frame subjected to horizontal load W, from table 39 is:
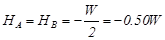
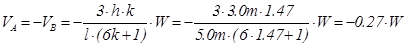
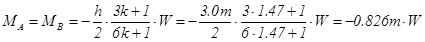
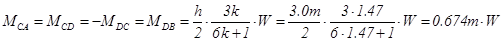
For load g=33.0 kN/m:
MA,g=-MB,g =0.60m2×33.0kN/m=19.8 kNm
MCA,g =MCD,g =MDC,g =-MDB,g =-1.20m2×33.0kN/m =-39.6 kNm,
HA,g =-HB,g =0.60m×33.0kN/m=19.8 kN, VA,g =VB,g =2.50m×33.0kN/m=82.5 kN
For load q=10.0 kN/m:
MA,q=-MB,q =0.60m2×10.0kN/m=6.0 kNm, MCA,q =MCD,q =MDC,q =-MDB,q =-1.20m2×10.0kN/m=-12.0 kNm,
HA,q =-HB,q =0.60m×10.0kN/m=6.0 kN, VA,q =VB,q =2.50m×10.0kN/m=25.0 kN
For load W=122.0 kN:
MA,W=MB,W =-0.826m×122.0kN=-100.8 kNm, MCA,W =MCD,W =-MDC,W =MDB,W =0.674×122.0=82.2 kNm,
HA,W =HB,W =-0.50×122.0kN=-61.0 kN, VA,W =-VB,W =-0.27×122.0kN=-32.9 kN