Ασκήσεις

Στον τυπικό όροφο πολυώροφου κτιρίου, το κέντρο μάζας ευρίσκεται στη θέση X=9.0, Y=9.0 και το σεισμικό φορτίο στο ισόγειο είναι 2000 kN. Για σεισμό κατά τη διεύθυνση X, ζητείται ο υπολογισμός των παραμορφώσεων και των εντάσεων των υποστυλωμάτων C₁, C₃, C₄, C₆, C₁₁, C₁₃, C₁₆ του ισογείου που έχει ύψος 3.0 m. Σκυρόδεμα C30/37.

Όποια και αν είναι η κατανομή των δυσκαμψιών ή η απόκλιση του Κέντρου Μάζας από το Κέντρο Ελαστικής Στροφής, το άθροισμα των τεμνουσών δυνάμεων κάθε διεύθυνσης θα είναι ίσο με την αντίστοιχη σεισμική δύναμη, δηλαδή στο συγκεκριμένο παράδειγμα Σ(V_x)=2000 kN και Σ(V_y) =0.

Στο φορέα της άσκησης 1, ζητείται η μετακίνηση του κέντρου ελαστικής στροφής κάθε ορόφου και η μέγιστη μετακίνηση του υψηλότερου ορόφου του κτιρίου όταν ο αριθμός των ορόφων εί-ναι 10 και το ύψος καθενός 3.0 m, στις δύο περιπτώσεις: (α) ορθογωνική κατανομή των σει-σμικών δυνάμεων και (β) τριγωνική κατανομή των σεισμικών δυνάμεων.

Σεισμική τέμνουσα βάσης = 2000 kN, ορθογωνική κατανομή σεισμικών δυνάμεων

Συμπεράσματα:

• • Η μεγαλύτερη απόλυτη μετακίνηση γίνεται στη 10^η στάθμη, όπου προκύπτει δ₁₀=55a και η μικρότερη στη 1^η στάθμη, όπου δ₁=10a. Αντίθετα, η μεγαλύτερη σχετική μετακίνηση γίνεται στην 1^η στάθμη, είναι δ_z1=10a και η μικρότερη στη 10^η στάθμη με δ_z10 =a.
• • Η μεγαλύτερη ένταση προκύπτει στην 1^η στάθμη λόγω της μεγαλύτερης σχετικής μετακίνησης και η μικρότερη στη 10^η στάθμη.
• • Οι ροπές ροπές των διαφραγμάτων, λόγω απόκλισης κέντρου βάρους-κέντρου ελαστικής στροφής, είναι ανάλογες των τεμνουσών δυνάμεων και οι αντίστοιχες μετακινήσεις είναι ανάλογες των μετακινήσεων των κέντρων ελαστικής στροφής, άρα η μεγαλύτερη μετακίνηση γίνεται στη 10^η στάθμη στο υποστύλωμα c13 και είναι 55/10=5.5 φορές μεγαλύτερη αυτής του ισογείου, δηλαδή δ_xx,10,13=5.5×5.60=30.8 mm και δ_xy,10,13=5.5×0.97=5.3 mm .

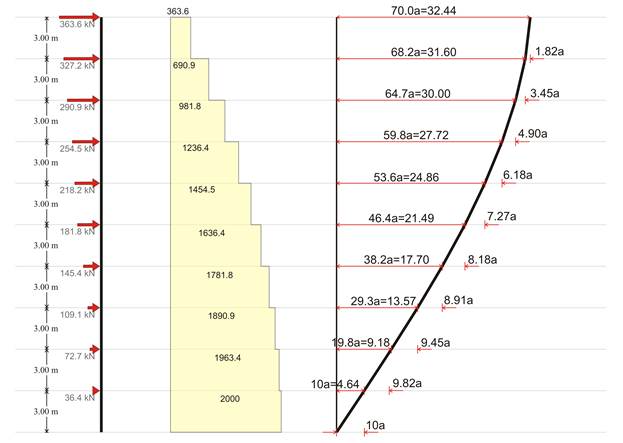
Σεισμική τέμνουσα βάσης = 2000 kN, τριγωνική κατανομή σεισμικών δυνάμεων

Συμπεράσματα:

·         Στην 1^η στάθμη, τόσο η τριγωνική, όσο και η ορθογωνική, αλλά και κάθε άλλη κατανομή των σεισμικών δυνάμεων, δίνει ίδια μετακίνηση και ίδια ένταση.

·         Για την ίδια σεισμική τέμνουσα, στην τριγωνική κατανομή έχουμε μεγαλύτερη μετακίνηση στον τελευταίο όροφο δ₁₀=70a ορόφου, έναντι δ₁₀=55a της ορθογωνικής κατανομής.

·         Το εμβαδόν του διαγράμματος των τεμνουσών δυνάμεων και υψών, που αντιπροσωπεύει τη συνολική ροπή των ορόφων, είναι μεγαλύτερο στην τριγωνική κατανομή απ’ ότι στην ορθογωνική.

H μεγαλύτερη μετακίνηση γίνεται στη 10^η στάθμη, στο υποστύλωμα c 13 και είναι 70/10=7.0 φορές μεγαλύτερη αυτής του ισογείου, δηλαδή δ_xx,10,13=7.0×5.60=39.2 mm και δ_xy,10,13=7.0×0.97=6.8 mm.

Σεισμός με τέμνουσα βάσης 2000 kN και ορθογωνική κατανομή των σεισμικών δυνάμεων

Ο πραγματικός σκελετός του κτιρίου με το wireframe προσομοίωμα

Στον προηγούμενο όροφο της άσκησης 1, να βρεθούν τα αντίστοιχα αποτελέσματα αν αντικα-τασταθούν τα υποστυλώματα C3, C5, C12, C14 με τοιχία διατομής 2000/300 παράλληλα προς την κάθε πλευρά της περιμέτρου.

Στον όροφο της άσκησης 1 να βρεθούν τα αντίστοιχα αποτελέσματα στις παρακάτω περιπτώσεις: (α) αντικατάσταση των υποστυλωμάτων C₅, C₁₂, C₁₄  με  τοιχία διατομής 2000/300 παράλληλα προς τις αντίστοιχες πλευρές της περιμέτρου.

(β) αντικατάσταση των υποστυλωμάτων C₁₂, C₁₄,  με  τοιχία διατομής 2000/300 παράλληλα προς τις αντίστοιχες πλευρές της περιμέτρου.

δ) αντικατάσταση του υποστυλώματος C5 με τοιχίο διατομής 2000/300 παράλληλο προς την αντίστοιχη πλευρά της περιμέτρου.

(d) replacement of the column C5 with wall of cross-section 2000/300 in parallel to the respec-tive side of the perimeter.