(μελέτη <B_531>)
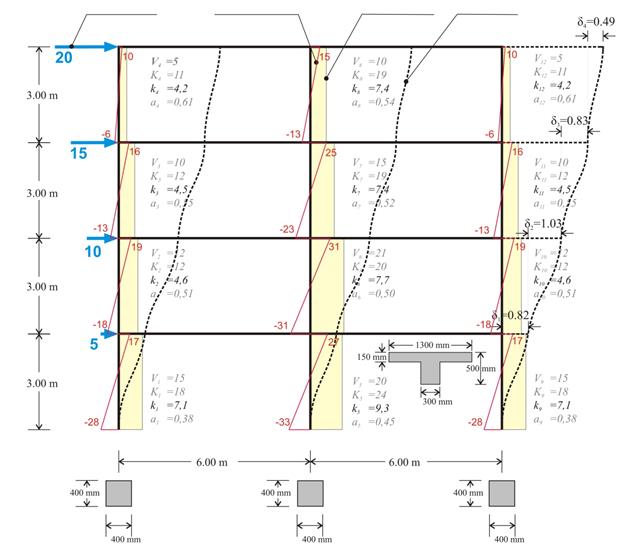
Στο επίπεδο πολυώροφο πλαίσιο της εικόνας, φαίνεται η διακύμανση του φαινομένου συντελεστή δυσκαμψίας kj και του συντελεστή κατανομής ροπής aj σε ακραία και μεσαία κολόνα από όροφο σε όροφο.
Οι φαινόμενοι συντελεστές δυσκαμψίας kj κυμαίνονται μεταξύ 4 και 9, ενώ οι συντελεστές κατανομής της ροπής aj μεταξύ 0.40 και 0.60.
Οι φαινόμενες δυσκαμψίες, δεν εξαρτώνται από το μέγεθος των σεισμικών φορτίων. Εξαρτώνται μόνο από την κατανομή των φορτίων καθ’ ύψος του πλαισίου. Αυτός είναι και ο λόγος που στα ακόλουθα παραδείγματα, τόσο οι δυνάμεις, οι τέμνουσες, οι ροπές, όσο και οι παραμορφώσεις δεν έχουν μονάδες μέτρησης.
Το χαρακτηριστικό μέγεθος της σεισμικής δράσης είναι η συνολική οριζόντια δύναμη, που ονομάζεται “τέμνουσα βάσης” επειδή ισούται με το άθροισμα των τεμνουσών δυνάμεων όλων των κολονών στη βάση του κτιρίου. Στο συγκεκριμένο παράδειγμα η τέμνουσα βάσης ισούται με 50, ενώ έχει εφαρμοστεί η τριγωνική κατανομή. Αν εφαρμοσθούν οι ίδιες συνολικά οριζόντιες δυνάμεις Vbase=50 με ορθογωνική ισοκατανομή, δηλαδή οριζόντιο φορτίο H=12.5 σε κάθε στάθμη, τα αποτελέσματα διαφέρουν κατά ένα μικρό ποσοστό της τάξης του 5%.
Σε περίπτωση υπογείου, οι σεισμικές δυνάμεις στην οροφή του είναι μηδενικές. Ωστόσο, η κατάσταση πλήρους πάκτωσης στη βάση των κολονών ισχύει μόνο για τις κολόνες που συντρέχουν στα περιμετρικά τοιχία του υπογείου.
Αν στο πλαίσιο υπάρχουν και τοιχία, όπως φαίνεται στην επόμενη παράγραφο, οι δυσκαμψίες και οι κατανομές των ροπών των τοιχίων διαφέρουν μεταξύ τους. Η διαφορά αυτή είναι τόσο πιο έντονη, όσο αυξάνει ο αριθμός των ορόφων.
Η επίλυση του πλαισίου δίνει τις συνολικές μετακινήσεις των κόμβων και τις εντάσεις των κολονών (τέμνουσες δυνάμεις και ροπές κάμψης). Τα μεγέθη K, k και a είναι παράγωγα των προηγούμενων αποτελεσμάτων. Η φαινόμενη δυσκαμψία Ki του ορόφου i προκύπτει από τη σχέση Ki=Vi/δi, ενώ η φαινόμενη δυσκαμψία της κολόνας j του ορόφου i από τη σχέση Ki,j=Vi,j/δi.
Παράδειγμα (3ος όροφος):
Δυσκαμψίες κολονών: K3,1=9.6/0.823=12, K3,2=15.8/0.823=19, K3,3=9.6/0.823=12.
Δυσκαμψία ορόφου: Κ3=(20+15)/0.823=43. Η ίδια τιμή προκύπτει αν την υπολογίσουμε και ως το άθροισμα των δυσκαμψιών των κολονών του ορόφου, δηλαδή K3= K3,1+K3,2+ K3,3=43.
Αν ληφθεί υπόψη η επιρροή των τεμνουσών δυνάμεων (Shear effect=ON), οι μετατοπίσεις προκύπτουν ίσες με δ1=0.85, δ2=1.05, δ3=0.84, δ4=0.50 mm, δηλαδή αμελητέα διαφορά.
Λαμβάνοντας όμως υπόψη και την επιρροή των στερεών σωμάτων (Rigid body=ON), οι μετατοπίσεις ισούνται με δ1=0.80, δ2=0.97, δ3=0.77, δ4=0.45 mm, μικρή μεν, αλλά μετρήσιμη διαφορά μικρότερων μετατοπίσεων και ισχυρότερων δυσκαμψιών.
a