Η επιρροή της στρεπτικής δυστρεψίας

Παραμορφωμένη κατάσταση φορέα (φορτία οριακής κατάστασης αστοχίας)

Στη μελέτη <B_334-1> του συνοδευτικού λογισμικού, η στηρίζουσα δοκός b1 έχει διατομή 300/500 και άνοιγμα l₁=4.0 m, ενώ η στηριζόμενη δοκός b2 επί της b1 έχει την ίδια διατομή 300/500 και άνοιγμα l₂=5.0 mm.

Διάγραμμα ροπών κάμψης συνολικού φορέα

Αν η ενεργή δυστρεψία της στηρίζουσας δοκού ληφθεί ίση με το 100% της πλήρους ελαστικής δυστρεψίας της, τότε η ροπή κάμψης στην αριστερή (έμμεση) στήριξη της στηριζόμενης δοκού b2 προκύπτει ίση με M=-40.4 kNm.

Η στηριζόμενη δοκός b2 θα πρέπει, στη μεν αριστερή (έμμεση) στήριξη να διαστασιολογηθεί για καμπτική ροπή M=-40.4 kNm και να οπλιστεί με μέλη στην άνω ίνα, οι οποίες θα πρέπει να αγκυρωθούν εντός της στηρίζουσας δοκού b1, στο δε άνοιγμα να διαστασιολογηθεί με καμπτική ροπή M=87.9 kNm και να οπλισθεί με μέλη στην κάτω ίνα. Η καμπτική ροπή της στηριζόμενης δοκού b2 δημιουργεί ροπή στρέψης M_T=M/2=40.4/2=20.2 kNm στη στηρίζουσα δοκό b1, όπως φαίνεται στο αντίστοιχο διάγραμμα στρεπτικών ροπών. Συμπεραίνουμε, λοιπόν, ότι η στηρίζουσα δοκός b1 θα πρέπει να διαστασιολογηθεί έναντι στρέψης.

Αν ο φορέας οπλιστεί κατάλληλα και οι ξυλότυποι παραμείνουν στη θέση τους μετά τη σκυροδέτηση έως την εξάσκηση όλων των φορτίων σχεδιασμού, μόλις ο φορέας ξεκαλουπωθεί το στατικό σύστημα θα λειτουργήσει με τον τρόπο που έγινε ο υπολογισμός, δηλαδή ελαστικά. Κατόπιν, θα αρχίσει να πλαστικοποιείται η δοκός b1 λόγω ερπυσμού. Στην πλαστικοποίηση συμβάλλει και η έλλειψη αρνητικού οπλισμού, ή η μη σωστή αγκύρωσή του.

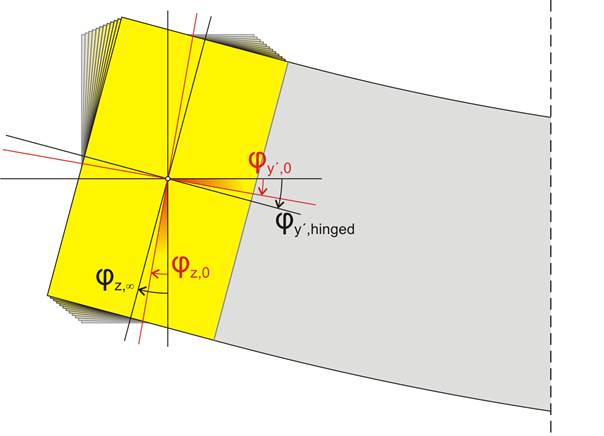
φ_z,0: η ελαστική γωνιακή παραμόρφωση τη χρονική στιγμή t=0
φ_z,∞: η γωνιακή παραμόρφωση τη χρονική στιγμή t=∞

Η γωνία στροφής της στηρίζουσας δοκού b1 στο σύστημα xyz (φ_z,0) θα ισούται με τη γωνία στροφής της στηριζόμενης δοκού b2 στο σύστημα x’y’z’ (φ_y’,0), δηλαδή θα ισχύει ότι φ_z,0=φ_y’,0.

Η γωνία στροφής φ_z,t της στηρίζουσας δοκού b1 θα αυξάνεται με την πάροδο χρόνου t, λόγω ερπυσμού. Καθώς ισχύει πάντοτε φ_y’,t=φ_z,t, θα αυξάνεται και η ισοδύναμη γωνία φ_y’,t της στηριζόμενης δοκού b2. Κατά συνέπεια, θα μειώνεται η ροπή κάμψης M και η ισοδύναμη ροπή στρέψης M_T, καθώς ισχύει πάντοτε M_T=M. Σε μία χρονική στιγμή t=∞, το σύστημα θα ισορροπήσει σε γωνία φ_y’,∞=φ_z,∞, η οποία δεν μπορεί να υπερβαίνει τη γωνία φ_y’,hinged. Η φ_y’,hinged αντιστοιχεί στην εφαπτομένη της ελαστικής γραμμής της στηριζόμενης δοκού b2 στο αριστερό άκρο, όταν η στήριξη εκεί μεταπέσει σε άρθρωση (M_T=M=0).

Αυτός είναι και ο λόγος για τον οποίο ο κανονισμός [EC2, §5.3.2.2(2)] επιτρέπει να λαμβάνεται γενικά αρθρωτή στήριξη τόσο στις στηρίξεις δοκών, όσο και στις στηρίξεις πλακών. Σε αντίθετη περίπτωση, θα πρέπει να λαμβάνεται υπόψη ο ερπυσμός, ή ενεργή δυσκαμψία ίση με ένα μικρό  ποσοστό (π.χ. 10%) της πλήρους ελαστικής.

Η θεώρηση μηδενικής δυστρεψίας δίνει λύση στην περίπτωση της αμφιέρειστης στηριζόμενης δοκού. Στην περίπτωση του προβόλου όμως, κάτι τέτοιο δεν ισχύει, διότι ο ισοστατικός φορέας μετατρέπεται σε μηχανισμό με το μηδενισμό της στροφής και τη μετατροπή της πάκτωσης σε άρθρωση.

Διαγράμματα ροπών συνολικού φορέα

Στην περίπτωση της αμφιέρειστης στηριζόμενης δοκού b2 με ενεργή δυστρεψία 1% της αντίστοιχης πλήρους ελαστικής, η έμμεση στήριξη της b2 επί της b1, πρακτικά, συμπεριφέρεται ως άρθρωση και δε μεταφέρει ροπή στρέψης στη στηρίζουσα δοκό b1. H b2 θα πρέπει να διαστασιολογηθεί μόνο για την καμπτική ροπή ανοίγματος M=110.9 kNm, σημαντικά μεγαλύτερη της ροπής 87.9 kNm της προηγούμενης περίπτωσης με ενεργή δυστρεψία ίση με το 100% της πλήρως ελαστικής.

Ενεργή δυστρεψία ίση με το 1% της ελαστικής, μελέτη <B_334-2>
 ροπές κάμψης, ‚ ροπές στρέψης

Η στήριξη της δοκού εν προβόλω, επί της φέρουσας δοκού πλαισίου, συμπεριφέρεται ως πλήρης πάκτωση και μεταφέρει όλη τη ροπή πάκτωσης (-64.1 kNm) ως ροπή στρέψης στη φέρουσα δοκό.

Σε ισοστατικό σε στρέψη φορέα, όπως ο φορέας II, όσο μικρή και αν είναι η δυστρεψία της φέρουσας δοκού, οι στρεπτικές ροπές παραμένουν ακέραιες.

• ·         Γενικά, η δυστρεψία των δοκών, τουλάχιστον σε χυτευόμενους σκελετούς (on site casting), καλό είναι να λαμβάνεται πολύ μικρή.

• ·         Αντίστοιχη λειτουργία προβλέπεται και στη στήριξη πλάκας επί δοκού όπως φαίνεται στην επόμενη παράγραφο.