Exercises (es-ES)

p=1.35g+1.50q=1.35×5.25+1.50×5.00=14.59 kN/m²

Given: Covering load g_e=1.00 kN/m², live load q=5.00 kN/m²,

concrete quality C30/37 (E=32.8 GPa).

Question: Perform static analysis to determine bending moments, shear forces, support reaction forces and elastic deflection

Solution:

M_x=12.9 kNm, M_y=7.6 kNm          V_x=22.1 kN, V_y=20.1 kN                           y=-1.73 mm

Bending moment distribution M₁₁          Shear force distribution V₁₁                       Deflections

Given: Covering load g_e=1.5 kN/m², live load q=2.0 kN/m², concrete quality C40/50 (E=35.2 GPa).

Question: Perform static analysis to calculate bending moments, shear forces, reaction forces, deflections and equivalent uniform loadings of slabs transferred onto beams.

Solution:

Bending moment diagram

Shear forces diagram

Deflections

Bending moment distribution M₁₁

Shear force distribution V₁₁

Deflections

Given: Covering load g_e=1.00 kN/m², live loads of domestic use q₁=q₂=2.00 kN/m², q₃=5.00 kN/m², concentrated load applied at the free end of the cantilever G₃=1.00 kN/m.

Question: Perform static analysis for the slabs illustrated in the figure (a) under global loading and (b) taking into account the effect of live loads.

Solution:

In ULS, the minimum design load for each slab i is equal to g_d,i=1.00·g, whereas the total design load is equal to p_d,i=γ_g·g_i+γ_q·q_i. In this case g_d,i=1.00·5.00=5.0 kN/m and G_d,3=1.00·1.0 kN (concentrated load). The maximum design load for the first two slabs is equal to p_d,1=p_d,2=1.35·5.00+1.50·2.00=9.75 kN/m, while for the third’s slab  (balcony) is equal to p_d,3=1.35·5.00+1.50·5.00=14.25 kN/m και P_d,3=1.35·1.00=1.35 kN.

ULS design load is applied simultaneously on each slab.

For this particular structure, the following six unfavourable loadings cases are required.

For each loading case the expressions giving the solution are identical:

M₁₀=-p₁·l₀₁²/8, M₂=-p₃·l₂₃²/2-P₃·l₂₃, M₁₂=-p₂·l₁₂²/8-M₂/2, M₁=(M₁₀+M₁₂)/2,
V₀₁=p₁·l₀₁/2+M₁/l₀₁, V₁₀=-p₁·l₀₁/2+M₁/l_{01 ,} V₁₂=p₂·l₁₂/2+(M₂-M₁)/l₁₂, V₂₁=-p₂·l₁₂/2+(M₂-M₁)/l₁₂

V₂₃=p₃·l₂₃+P₃, V₃₂=P₃

maxM₀₁=V₀₁²/(2·p₁), maxM₁₂=V₁₂²/(2·p₂)+M₁maxM₀₁=V₀₁²/(2·p₁),  maxM₁₂=V₁₂²/(2·p₂)+M₁

The global loading diagram is illustrated with dashed line p_d=1.35×g+1.50×q

Given: Covering load g_επ=1.5 kN/m², live load q=5.0 kN/m², concrete quality C40/50.

Question

: Perform static analysis of the slabs illustrated in the figure (shears forces, bending moments, deflections) using the finite element method with (a) global loading and (b) unfavourable loadings.

Bending moment diagram

M_x=13.9 kNm, M_y=12.4 kNm, M_yerm=-34.6 kNm

Shear force diagram

V_xr=23.6 kN, V_yr=24.1 kN, V_yerm=45.5 kN

Deflection diagram

y_max=4.03 mm

Deflection diagrams and contours

Bending moment diagrams

M_x=15.5 kNm, M_y=12.4 kNm, M_yerm=-34.6 kNm

Shear force diagrams
Vxr=24.8 kN, Vyr=24.5 kN, Vyerm=45.5 kN

Deflection diagrams

y_max=4.39 mm

Deflection diagrams and contours

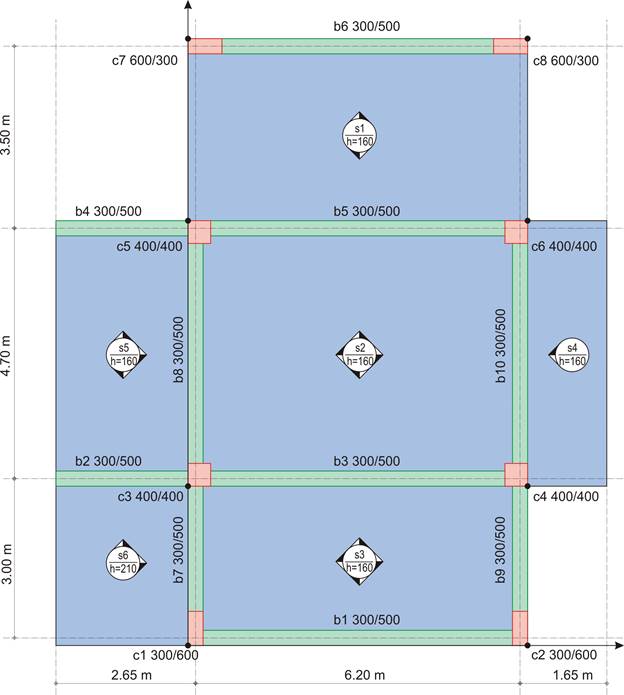
Given: Thickness of slabs s1, s2, s3, s4, s5: h=160 mm, s6: h=210 mm and covering load g_επ=2.0 kN/m².

Question: Perform static analysis to determine the distribution of slabs loads transferred onto beams

Static analysis

g_1,2,3,4,5=0.16·1.0x25.0=4.0 kN/m², g₆=0.21·1.0x25.0=5.25 kN/m², g_επ=2.0 kN/m²

Analysis will be performed using the global load (due to the small value of the live load):

p_1,2,3,4,5=6.0·1.35+2.0·1.5=11.1 kN/m², p₆=7.25·1.35+2.0·1.5=12.80 kN/m²

Thus, on 1.0 m wide strips, the respective loads are p_{1, 2,3,4,5}=11.1 kN/m and p₆=12.80 kN/m

επομένως, σε ζώνη πλάτους 1.0 m, αντιστοιχεί φορτίοp_1,2,3,4,5=11.1 kN/m και p₆=12.80 kN/m.

In general, the most unfavourable span moments, arise in one-way slabs (s1) or cantilever slabs (s4) at one point in the first direction and at one line in the other. In two-way slabs moments are developed at the same point in both directions.